McqMate
| Q. |
Consider the graph M with 3 vertices. Its adjacency matrix is shown below. Which of the following is true?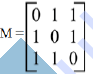
|
| A. | graph m has no minimum spanning tree |
| B. | graph m has a unique minimum spanning trees of cost 2 |
| C. | graph m has 3 distinct minimum spanning trees, each of cost 2 |
| D. | graph m has 3 spanning trees of different costs |
| Answer» C. graph m has 3 distinct minimum spanning trees, each of cost 2 | |
| Explanation: here all non-diagonal elements in the adjacency matrix are 1. so, every vertex is connected every other vertex of the graph. and, so graph m has 3 distinct minimum spanning trees. | |
1.9k
0
Do you find this helpful?
4
View all MCQs in
Design and Analysis of AlgorithmsDiscussion
No comments yet
Related MCQs
- A k-regular bipartite graph is the one in which degree of each vertices is k for all the vertices in the graph. Given that the bipartitions of this graph are U and V respectively. What is the relation between them?
- Consider the graph shown below. Which of the following are the edges in the MST of the given graph?
- Which of the following is not an Eigen value of the adjacency matrix of the complete bipartite graph?
- Consider a undirected graph G with vertices { A, B, C, D, E}. In graph G, every edge has distinct weight. Edge CD is edge with minimum weight and edge AB is edge with maximum weight. Then, which of the following is false?
- What is the multiplicity for the adjacency matrix of complete bipartite graph for 0 Eigen value?
- Consider a complete graph G with 4 vertices. The graph G has spanning trees.
- A complete bipartite graph is a one in which each vertex in set X has an edge with set Y. Let n be the total number of vertices. For maximum number of edges, the total number of vertices hat should be present on set X is?
- From the given graph, how many vertices can be matched using maximum matching in bipartite graph algorithm?
- Matrix A is of order 3*4 and Matrix B is of order 4*5. How many elements will be there in a matrix A*B multiplied recursively.
- If Matrix X is of order A*B and Matrix Y is of order C*D, and B=C then the order of the Matrix X*Y is A*D?