McqMate
179
98.7k
410+ Design and Analysis of Algorithms Solved MCQs
These multiple-choice questions (MCQs) are designed to enhance your knowledge and understanding in the following areas: Computer Science Engineering (CSE) .
| 101. |
The most important condition for which closest pair is calculated for the points (pi, pj) is? |
| A. | i>j |
| B. | i!=j |
| C. | i=j |
| D. | i<j |
| Answer» D. i<j | |
| Explanation: to avoid computing the distance between the same pair of points twice, we consider only the pair of points (pi, pj) for which i<j. | |
| 102. |
What is the basic operation of closest pair algorithm using brute force technique? |
| A. | euclidean distance |
| B. | radius |
| C. | area |
| D. | manhattan distance |
| Answer» A. euclidean distance | |
| Explanation: the basic operation of closest | |
| 103. |
Which of the following is similar to Euclidean distance? |
| A. | manhattan distance |
| B. | pythagoras metric |
| C. | chebyshev distance |
| D. | heuristic distance |
| Answer» B. pythagoras metric | |
| Explanation: in older times, euclidean distance metric is also called a pythagoras metric which is the length of the line segment connecting two points. | |
| 104. |
Which of the following strategies does the following diagram depict? |
| A. | divide and conquer strategy |
| B. | brute force |
| C. | exhaustive search |
| D. | backtracking |
| Answer» B. brute force | |
| Explanation: brute force is a straight forward approach to solve critical problems. here, we use brute force technique to find the closest distance between p1 and p2. | |
| 105. |
Manhattan distance is an alternative way to define a distance between two points. |
| A. | true |
| B. | false |
| Answer» A. true | |
| Explanation: manhattan distance is an alternative way to calculate distance. it is the distance between two points measured along axes at right angles. | |
| 106. |
What is the optimal time required for solving the closest pair problem using divide and conquer approach? |
| A. | o(n) |
| B. | o(log n) |
| C. | o(n log n) |
| D. | o(n2) |
| Answer» C. o(n log n) | |
| Explanation: the optimal time for solving using a divide and conquer approach is mathematically found to be o(n log n). | |
| 107. |
In divide and conquer, the time is taken for merging the subproblems is? |
| A. | o(n) |
| B. | o(n log n) |
| C. | o(n2) |
| D. | o(log n) |
| Answer» B. o(n log n) | |
| Explanation: the time taken for merging the smaller subproblems in a divide and conquer approach is mathematically found to be o(n log n). | |
| 108. |
The optimal time obtained through divide and conquer approach using merge sort is the best case efficiency. |
| A. | true |
| B. | false |
| Answer» A. true | |
| Explanation: the optimal time obtained through divide and conquer approach is the best class efficiency and it is given by Ω(n log n). | |
| 109. |
Which of the following strategies does the following diagram depict? |
| A. | brute force |
| B. | divide and conquer |
| C. | exhaustive search |
| D. | branch and bound |
| Answer» B. divide and conquer | |
| Explanation: the above diagram depicts the implementation of divide and conquer. the problem is divided into sub problems and are separated by a line. | |
| 110. |
Which of the points are closer to each other? |
| A. | p1 and p11 |
| B. | p3 and p8 |
| C. | p2 and p3 |
| D. | p9 and p10 |
| Answer» C. p2 and p3 | |
| Explanation: from symmetry, we determine that the closest pair is p2 and p3. but the exact calculations have to be done using euclid’s algorithm. | |
| 111. |
Cross product is a mathematical operation performed between |
| A. | 2 scalar numbers |
| B. | a scalar and a vector |
| C. | 2 vectors |
| D. | any 2 numbers |
| Answer» C. 2 vectors | |
| Explanation: cross product is a mathematical operation that is performed on 2 vectors in a 3d plane. it has many applications in computer programming and physics. | |
| 112. |
Cross product is also known as? |
| A. | scalar product |
| B. | vector product |
| C. | dot product |
| D. | multiplication |
| Answer» B. vector product | |
| Explanation: cross product is also known as a vector product. it is a mathematical operation that is performed on 2 vectors in 3d plane. | |
| 113. |
The concept of cross product is applied in the field of computer graphics. |
| A. | true |
| B. | false |
| Answer» A. true | |
| Explanation: the concept of cross product find its application in the field of computer graphics. it can be used to find the winding of polygon about a point. | |
| 114. |
Which of the following equals the a x b ( a and b are two vectors)? |
| A. | – (a x b) |
| B. | a.b |
| C. | b x a |
| D. | – (b x a) |
| Answer» D. – (b x a) | |
| Explanation: the vector product a x b is equal to – (b x a). the minus sign shows that these vectors have opposite directions. | |
| 115. |
Cross product of two vectors can be used to find? |
| A. | area of rectangle |
| B. | area of square |
| C. | area of parallelogram |
| D. | perimeter of rectangle |
| Answer» C. area of parallelogram | |
| Explanation: cross product of two vectors can be used to find the area of parallelogram. for this, we need to consider the vectors as the adjacent sides of the parallelogram. | |
| 116. |
What will be the cross product of the vectors 2i + 3j + k and 3i + 2j + k? |
| A. | i + 2j + k |
| B. | 2i + 3j + k |
| C. | i + j – 5k |
| D. | 2i – j – 5k |
| Answer» C. i + j – 5k | |
| Explanation: we can find the cross product of the given vectors by solving the determinant. | |
| 117. |
What will be the cross product of the vectors 2i + 3j + k and 6i + 9j + 3k? |
| A. | i + 2j + k |
| B. | i – j – 5k |
| C. | 0 |
| D. | 2i – j – 5k |
| Answer» C. 0 | |
| Explanation: the given vectors are parallel to each other. the cross product of parallel vectors is 0 because sin(0) is 0. | |
| 118. |
Which of the following operation will give a vector that is perpendicular to both vectors a and b? |
| A. | a x b |
| B. | a.b |
| C. | b x a |
| D. | both a x b and b x a |
| Answer» D. both a x b and b x a | |
| Explanation: the resultant vector from the cross product of two vectors is perpendicular to the plane containing both vectors. so both a x b and b x a will give a vector that is perpendicular to both vectors a and b. | |
| 119. |
is a method of constructing a smallest polygon out of n given points. |
| A. | closest pair problem |
| B. | quick hull problem |
| C. | path compression |
| D. | union-by-rank |
| Answer» B. quick hull problem | |
| Explanation: quick hull is a method of | |
| 120. |
What is the other name for quick hull problem? |
| A. | convex hull |
| B. | concave hull |
| C. | closest pair |
| D. | path compression |
| Answer» A. convex hull | |
| Explanation: the other name for quick hull problem is convex hull problem whereas the closest pair problem is the problem of finding the closest distance between two points. | |
| 121. |
How many approaches can be applied to solve quick hull problem? |
| A. | 1 |
| B. | 2 |
| C. | 3 |
| D. | 4 |
| Answer» B. 2 | |
| Explanation: most commonly, two approaches are adopted to solve quick hull problem- brute force approach and divide and conquer approach. | |
| 122. |
What is the average case complexity of a quick hull algorithm? |
| A. | o(n) |
| B. | o(n log n) |
| C. | o(n2) |
| D. | o(log n) |
| Answer» B. o(n log n) | |
| Explanation: the average case complexity of quickhull algorithm using divide and conquer approach is mathematically found to be o(n log n). | |
| 123. |
What does the following diagram depict? |
| A. | closest pair |
| B. | convex hull |
| C. | concave hull |
| D. | path compression |
| Answer» B. convex hull | |
| Explanation: the above diagram is a depiction of convex hull, also known as quick hull, since it encloses n points into a convex polygon. | |
| 124. |
The quick hull algorithm runs faster if the input uses non- extreme points. |
| A. | true |
| B. | false |
| Answer» A. true | |
| Explanation: it is proved that the quick hull algorithm runs faster if the input uses non- | |
| 125. |
To which type of problems does quick hull belong to? |
| A. | numerical problems |
| B. | computational geometry |
| C. | graph problems |
| D. | string problems |
| Answer» B. computational geometry | |
| Explanation: quick hull problem and closest pair algorithms are some of the examples of computational problems. | |
| 126. |
Who formulated quick hull algorithm? |
| A. | eddy |
| B. | andrew |
| C. | chan |
| D. | graham |
| Answer» A. eddy | |
| Explanation: eddy formulated quick hull algorithm. graham invented graham scan. andrew formulated andrew’s algorithm and chan invented chan’s algorithm. | |
| 127. |
The time is taken to find the ‘n’ points that lie in a convex quadrilateral is? |
| A. | o(n) |
| B. | o(n log n) |
| C. | o(n2) |
| D. | o(log n) |
| Answer» A. o(n) | |
| Explanation: the time taken to find the ‘n’ points that lie in a convex quadrilateral is mathematically found to be o(n). | |
| 128. |
What is the running time of Chan’s algorithm? |
| A. | o(log n) |
| B. | o(n log n) |
| C. | o(n log h) |
| D. | o(log h) |
| Answer» C. o(n log h) | |
| Explanation: the running time of chan’s algorithm is calculated to be o(n log h) where h is the number of vertices of the convex hull. | |
| 129. |
The running time of Chan’s algorithm is obtained from combining two algorithms. |
| A. | true |
| B. | false |
| Answer» A. true | |
| Explanation: the o(n log h) running time of chan’s algorithm is obtained by combining the running time of graham’s scan [o(n log n)] and jarvis match [o(nh)]. | |
| 130. |
Which of the following is called the “ultimate planar convex hull algorithm”? |
| A. | chan’s algorithm |
| B. | kirkpatrick-seidel algorithm |
| C. | gift wrapping algorithm |
| D. | jarvis algorithm |
| Answer» B. kirkpatrick-seidel algorithm | |
| Explanation: kirkpatrick-seidel algorithm is called as the ultimate planar convex hull algorithm. its running time is the same as that of chan’s algorithm (i.e.) o(n log h). | |
| 131. |
Which of the following algorithms is the simplest? |
| A. | chan’s algorithm |
| B. | kirkpatrick-seidel algorithm |
| C. | gift wrapping algorithm |
| D. | jarvis algorithm |
| Answer» A. chan’s algorithm | |
| Explanation: chan’s algorithm is very practical for moderate sized problems whereas kirkpatrick-seidel algorithm is not. although, they both have the same running time. gift wrapping algorithm is a non-output sensitive algorithm and has a longer running time. | |
| 132. |
What is the running time of Hershberger algorithm? |
| A. | o(log n) |
| B. | o(n log n) |
| C. | o(n log h) |
| D. | o(log h) |
| Answer» B. o(n log n) | |
| Explanation: hershberger’s algorithm is an output sensitive algorithm whose running | |
| 133. |
Which of the following is false in the case of a spanning tree of a graph G? |
| A. | it is tree that spans g |
| B. | it is a subgraph of the g |
| C. | it includes every vertex of the g |
| D. | it can be either cyclic or acyclic |
| Answer» D. it can be either cyclic or acyclic | |
| Explanation: a graph can have many spanning trees. each spanning tree of a graph g is a subgraph of the graph g, and spanning trees include every vertex of the gram. | |
| 134. |
Every graph has only one minimum spanning tree. |
| A. | true |
| B. | false |
| Answer» B. false | |
| Explanation: minimum spanning tree is a spanning tree with the lowest cost among all the spacing trees. sum of all of the edges in the spanning tree is the cost of the spanning tree. there can be many minimum spanning trees for a given graph. | |
| 135. |
Consider a complete graph G with 4 vertices. The graph G has spanning trees. |
| A. | 15 |
| B. | 8 |
| C. | 16 |
| D. | 13 |
| Answer» C. 16 | |
| Explanation: a graph can have many spanning trees. and a complete graph with n vertices has n(n-2) spanning trees. so, the complete graph with 4 vertices has 4(4-2) = 16 spanning trees. | |
| 136. |
The travelling salesman problem can be solved using |
| A. | a spanning tree |
| B. | a minimum spanning tree |
| C. | bellman – ford algorithm |
| D. | dfs traversal |
| Answer» B. a minimum spanning tree | |
| Explanation: in the travelling salesman problem we have to find the shortest possible route that visits every city exactly once and returns to the starting point for the given a set of cities. so, travelling salesman problem can be solved by contracting the minimum spanning tree. | |
| 137. |
Consider the graph M with 3 vertices. Its adjacency matrix is shown below. Which of the following is true?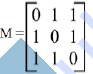
|
| A. | graph m has no minimum spanning tree |
| B. | graph m has a unique minimum spanning trees of cost 2 |
| C. | graph m has 3 distinct minimum spanning trees, each of cost 2 |
| D. | graph m has 3 spanning trees of different costs |
| Answer» C. graph m has 3 distinct minimum spanning trees, each of cost 2 | |
| Explanation: here all non-diagonal elements in the adjacency matrix are 1. so, every vertex is connected every other vertex of the graph. and, so graph m has 3 distinct minimum spanning trees. | |
| 138. |
Consider a undirected graph G with vertices { A, B, C, D, E}. In graph G, every edge has distinct weight. Edge CD is edge with minimum weight and edge AB is edge with maximum weight. Then, which of the following is false? |
| A. | every minimum spanning tree of g must contain cd |
| B. | if ab is in a minimum spanning tree, then its removal must disconnect g |
| C. | no minimum spanning tree contains ab |
| D. | g has a unique minimum spanning tree |
| Answer» C. no minimum spanning tree contains ab | |
| Explanation: every mst will contain cd as it is smallest edge. so, every minimum spanning tree of g must contain cd is true. and g has a unique minimum spanning tree is also true because the graph has edges with distinct weights. so, no minimum spanning tree contains ab is false. | |
| 139. |
If all the weights of the graph are positive, then the minimum spanning tree of the graph is a minimum cost subgraph. |
| A. | true |
| B. | false |
| Answer» A. true | |
| Explanation: a subgraph is a graph formed from a subset of the vertices and edges of the original graph. and the subset of vertices includes all endpoints of the subset of the edges. so, we can say mst of a graph is a subgraph when all weights in the original graph are positive. | |
| 140. |
Which of the following is not the algorithm to find the minimum spanning tree of the given graph? |
| A. | boruvka’s algorithm |
| B. | prim’s algorithm |
| C. | kruskal’s algorithm |
| D. | bellman–ford algorithm |
| Answer» D. bellman–ford algorithm | |
| Explanation: the boruvka’s algorithm, prim’s algorithm and kruskal’s algorithm are the algorithms that can be used to find the minimum spanning tree of the given graph. the bellman-ford algorithm is used to find the shortest path from the single source to all other vertices. | |
| 141. |
Which of the following is false? |
| A. | the spanning trees do not have any cycles |
| B. | mst have n – 1 edges if the graph has n edges |
| C. | edge e belonging to a cut of the graph if has the weight smaller than any other edge in the same cut, then the edge e is present in all the msts of the graph |
| D. | removing one edge from the spanning tree will not make the graph disconnected |
| Answer» D. removing one edge from the spanning tree will not make the graph disconnected | |
| Explanation: every spanning tree has n – 1 edges if the graph has n edges and has no cycles. the mst follows the cut property, edge e belonging to a cut of the graph if has the weight smaller than any other edge in the same cut, then the edge e is present in all the msts of the graph. | |
| 142. |
Consider the following graph. Using Kruskal’s algorithm, which edge will be selected first? |
| A. | gf |
| B. | de |
| C. | be |
| D. | bg |
| Answer» C. be | |
| Explanation: in krsuskal’s algorithm the edges are selected and added to the spanning tree in increasing order of their weights. | |
| 143. |
Which of the following edges form minimum spanning tree on the graph using kruskals algorithm? |
| A. | (b-e)(g-e)(e-f)(d-f) |
| B. | (b-e)(g-e)(e-f)(b-g)(d-f) |
| C. | (b-e)(g-e)(e-f)(d-e) |
| D. | (b-e)(g-e)(e-f)(d-f)(d-g) |
| Answer» A. (b-e)(g-e)(e-f)(d-f) | |
| Explanation: using krushkal’s algorithm on the given graph, the generated minimum spanning tree is shown below. | |
| 144. |
Which of the following is false about the Kruskal’s algorithm? |
| A. | it is a greedy algorithm |
| B. | it constructs mst by selecting edges in increasing order of their weights |
| C. | it can accept cycles in the mst |
| D. | it uses union-find data structure |
| Answer» C. it can accept cycles in the mst | |
| Explanation: kruskal’s algorithm is a greedy algorithm to construct the mst of the given graph. it constructs the mst by selecting edges in increasing order of their weights and rejects an edge if it may form the cycle. so, using kruskal’s algorithm is never formed. | |
| 145. |
Kruskal’s algorithm is best suited for the dense graphs than the prim’s algorithm. |
| A. | true |
| B. | false |
| Answer» B. false | |
| Explanation: prim’s algorithm outperforms the kruskal’s algorithm in case of the dense graphs. it is significantly faster if graph has more edges than the kruskal’s algorithm. | |
| 146. |
Which of the following is true? |
| A. | prim’s algorithm initialises with a vertex |
| B. | prim’s algorithm initialises with a edge |
| C. | prim’s algorithm initialises with a vertex which has smallest edge |
| D. | prim’s algorithm initialises with a forest |
| Answer» A. prim’s algorithm initialises with a vertex | |
| Explanation: steps in prim’s algorithm: (i) select any vertex of given graph and add it to mst (ii) add the edge of minimum weight from a vertex not in mst to the vertex in mst; (iii) it mst is complete the stop, otherwise go to step (ii). | |
| 147. |
Kruskal’s algorithm is best suited for the sparse graphs than the prim’s algorithm. |
| A. | true |
| B. | false |
| Answer» A. true | |
| Explanation: prim’s algorithm and kruskal’s algorithm perform equally in case of the sparse graphs. but kruskal’s algorithm is simpler and easy to work with. so, it is best suited for sparse graphs. | |
| 148. |
Prim’s algorithm can be efficiently implemented using for graphs with greater density. |
| A. | d-ary heap |
| B. | linear search |
| C. | fibonacci heap |
| D. | binary search |
| Answer» A. d-ary heap | |
| Explanation: in prim’s algorithm, we add the minimum weight edge for the chosen vertex which requires searching on the array of weights. this searching can be efficiently implemented using binary heap for dense graphs. and for graphs with greater density, prim’s algorithm can be made to run in linear time using d-ary heap(generalization of binary heap). | |
| 149. |
How many times the insert and extract min operations are invoked per vertex? |
| A. | 1 |
| B. | 2 |
| C. | 3 |
| D. | 0 |
| Answer» A. 1 | |
| Explanation: insert and extract min operations are invoked only once per vertex because each vertex is added only once to the set and each edge in the adjacency list is examined only once during the course of algorithm. | |
| 150. |
What is running time of Dijkstra’s algorithm using Binary min- heap method? |
| A. | o(v) |
| B. | o(vlogv) |
| C. | o(e) |
| D. | o(elogv) |
| Answer» D. o(elogv) | |
| Explanation: time required to build a binary min heap is o(v). each decrease key operation takes o(logv) and there are still at most e such operations. hence total running time is o(elogv). | |
Done Studing? Take A Test.
Great job completing your study session! Now it's time to put your knowledge to the test. Challenge yourself, see how much you've learned, and identify areas for improvement. Don’t worry, this is all part of the journey to mastery. Ready for the next step? Take a quiz to solidify what you've just studied.